Node Ranking
A crucial factor in determining a node's task selection probability within the Blockless network is its trust score, or node ranking. The trust score serves as an indicator of a node's trustworthiness and reliability compared to other nodes in the network.
To devise a node's trust score, Blockless employs the Elo rating system, developed by Hungarian-born American physicist Arpad Elo. Originally designed for ranking players in two-player games like chess, the Elo rating system is a skill-based system that measures the likelihood of a player winning a game against another player. In the context of Blockless, "winning a game" refers to the successful completion of a computational task.
The Elo rating system is adapted to assess and rank nodes based on their attributes and the probability outcome of completing computational tasks. This adaptation enables the system to account for factors such as processing power, memory capacity, energy efficiency, and overall performance in benchmark tests. By employing the Elo rating system, Blockless can dynamically and objectively rank nodes, ensuring that tasks are allocated to the most trustworthy and reliable nodes within the network. This, in turn, helps optimize the efficiency and security of the Blockless system.
Advantages of Applying Elo's System to Blockless Network
The Elo rating system offers several benefits when applied to the Blockless Network, making it a robust and flexible solution for ranking nodes based on their performance:
- Dynamic ranking: The Elo rating system is inherently dynamic, making it well-suited for ranking nodes in the Blockless Network, where technology and performance are constantly evolving. The system can easily adapt to the introduction of new nodes and changing performance levels, ensuring the ranking remains up-to-date and relevant.
- Objective comparison: The pairwise comparison approach enables a more objective comparison between nodes, as it directly measures their performance in head-to-head contests. This helps reduce the influence of subjective factors and biases on the ranking process, promoting a fair and accurate assessment of node performance.
- Customizable criteria: The Elo rating system can be tailored to specific needs by incorporating additional attributes and outcomes of computing or by applying different weightings to these factors. This adaptability allows for a customized ranking system that addresses the unique requirements of various users, industries, or use cases.
- Versatility: The Elo rating system can be applied to rank nodes across various segments and categories, from personal devices to high-performance computing clusters. This versatility makes it a valuable tool for evaluating and comparing computing performance across a wide range of applications.
Adapting Elo's System for Computer Ranking in Blockless
To effectively apply the Elo rating system for ranking nodes in the Blockless Network, it is essential to understand several key components of the system in the context of node performance:
- Defining attributes and outcomes of computing: The first step involves identifying relevant attributes and outcomes of computing that can be used to compare and rank nodes. These factors include processing power, memory capacity, energy efficiency, overall performance in benchmark tests, and the ability to complete tasks in a timely manner.
- Pairwise comparison: Drawing from the original Elo rating system, the adapted method requires pairwise comparison of nodes. To achieve this, a set of standardized tasks or benchmarks is defined, enabling the comparison of two nodes' performance in a head-to-head contest. The performance of each node in completing these tasks influences its rating.
- Performance expectation and updating ratings: In line with the principles of the Elo rating system, the performance expectation of each node is calculated based on their current ratings. After the head-to-head comparison, the ratings are updated according to the actual outcome of the comparison, taking into account the performance expectation.
The Blockless node ranking process is iterative, as nodes are continuously compared in various combinations to refine their ratings. This ongoing adaptation ensures that the ranking remains up-to-date as new nodes join the network or existing nodes improve their performance. This process optimizes task allocation and enhances the overall efficiency and reliability of the Blockless Network.
Adapting Elo's System with the Total Points Algorithm
The traditional Elo's system is defined as follows:
where
- : The updated rating of node A after the contest.
- : The current rating of node A before the contest.
- : The current rating of node B before the contest.
- : The actual score of node A in the contest (usually 1 for a win, 0.5 for a draw, and 0 for a loss).
- : A constant value, usually set between 10 and 60, that determines how much the rating should change after a contest. Higher values of K will result in larger rating changes.
- : Computes the expected score of node A based on the current ratings of nodes A and B. If the actual score of node A is higher than the expected score, node A's rating will increase, while if it's lower, node A's rating will decrease. The magnitude of the change depends on the value of K and the difference between the actual and expected scores.
The given algorithm is a generic scoring system used to compute the total points based on various factors. In this section, we will adapt the algorithm to evaluate computing performance considering the completeness of computing, time of response, and machine attributes matching compute requests. We will also discuss the algorithm's applicability in the context of computing performance assessment.
The adapted algorithm for evaluating computing performance can be represented as follows:
where:
- represents the points awarded for the completeness of computing tasks.
- represents the points awarded based on the time of response.
- represents the points awarded for the machine attributes that match compute requests.
- represents additional points based on other relevant factors.
Algorithm Application to Computing Performance Assessment:
The adapted algorithm allows for the evaluation of computing performance using a comprehensive scoring system. The various components of the algorithm are explained:
- Completeness of Computing : This factor measures the extent to which a computer can perform a given set of tasks. The algorithm assigns points based on the percentage of tasks completed successfully. A higher percentage of task completion results in more points, indicating better performance.
- Time of Response : The time of response is a crucial factor in assessing the performance of a computer. The algorithm assigns points inversely proportional to the time taken to complete tasks, with faster response times receiving higher points. This rewards computers that can deliver results more quickly.
- Machine Attributes Matching Compute Requests : In addition to the completeness of computing and response time, the algorithm also considers the relevance of the computer's attributes to the specific compute requests. Points are awarded for each attribute that matches the compute request requirements, with a higher total indicating a better-suited computer for the given tasks.
- Bonus Points: The algorithm may include additional bonus points based on other relevant factors that influence computing performance. These factors can be tailored to specific use cases or industries, allowing the algorithm to be customized as needed.
Execution Node Ranking Flow Overview
This diagram shows how the Elo ranking of Execution Nodes is updated based on their results.
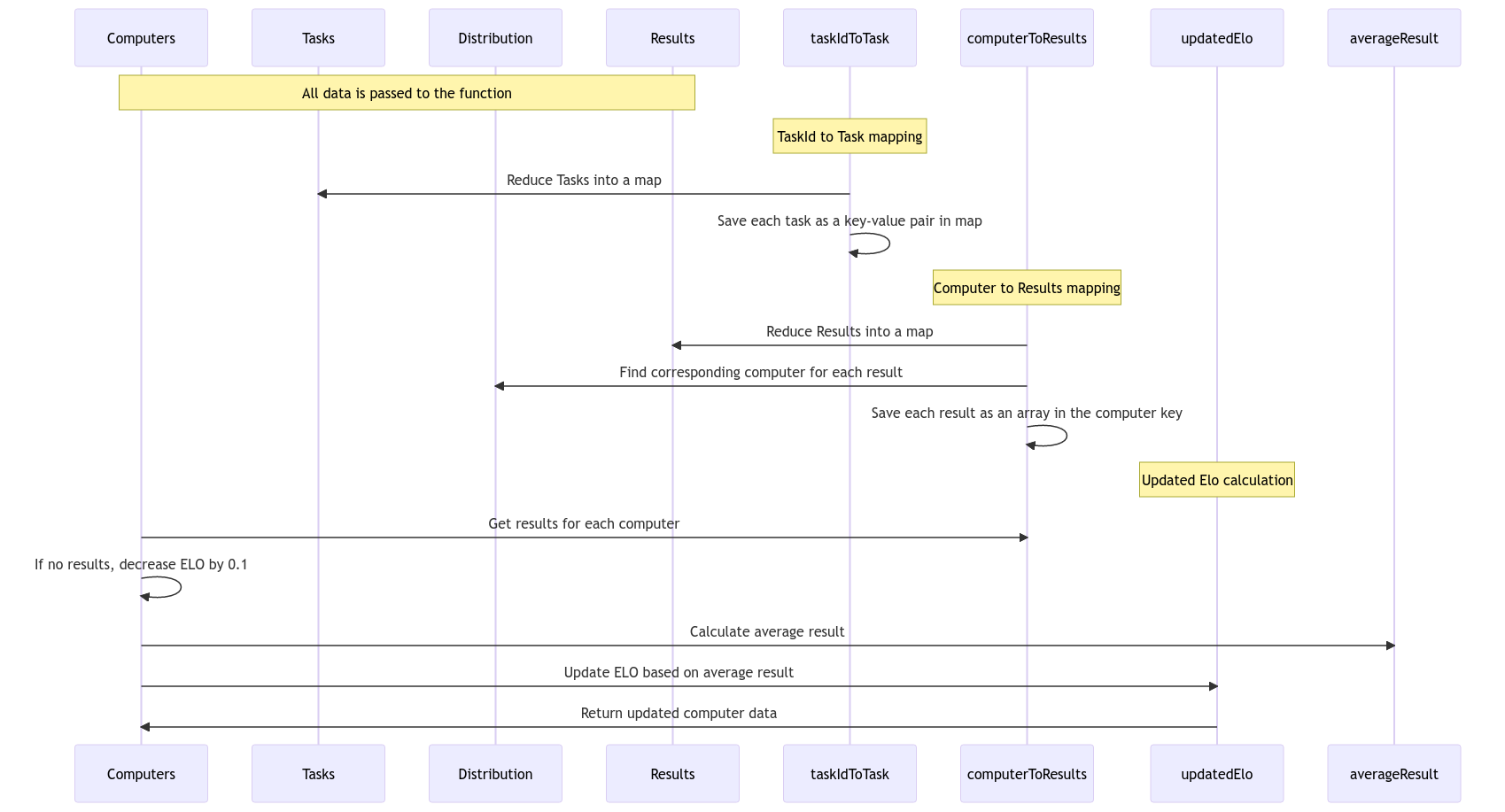
The process of updating the Elo ranking involves several steps that can be objectively described.
Firstly, the tasks are grouped into a map, with each task associated with its respective results. This enables the tracking of the different types of tasks performed and their outcomes.
Secondly, the results are reduced into another map, with each result linked to the computer that executed it. This step determines which computer performed each task and how well they performed it.
To calculate the Elo ranking for each computer, the results for each computer are retrieved, and the average performance score is calculated.
If a computer has not performed any tasks, its Elo ranking is not decreased. This is because the lack of tasks performed does not necessarily indicate a weaker performer but a lack of opportunity to perform tasks.
Once the average performance score for each computer is calculated, it is used to update the Elo ranking. The update involves a mathematical formula that considers the expected performance of a computer based on the Elo rankings of the other computers and compares it to the actual performance. The difference between the expected performance and the actual performance is used to update the Elo ranking for each computer.
Finally, the updated Elo ranking for each computer is returned, allowing for the determination of the better-performing computer and by how much.